TakasakiPhysicsClub-RoboCup-Documentation
著者：根岸孝次
ロボカップジュニアライトウェイトに出るにはマストとなるボールセンサについて解説します。ボールセンサと言っていますが、1つのセンサではなく、正確には多数の赤外線センサが集まったモージュルです。そこのところを履き違えないようにしてください。
赤外線センサ
残念ながら人間の目には赤外線が見えないのでセンサを使います。（そもそも人間に見えてもセンサを使うことには変わりないか）ボールが発行する赤外線の特徴や赤外線センサの特徴などを解説すると非常に疲れるのでこの資料では割愛します。気になる人はこのサイトを参考にすると良いと思います。
私がおすすめするのはTSSP58038です。先ほど紹介したサイトで理由は説明されているので割愛します。岡田先生の誤発注により物理部には大量に在庫があると思います。これを使いましょう。
ロボカップで赤外線センサを用いてボールをセンシングする方法として2種類あります。「パルス幅を監視する方法」と「ローパスフィルタを通してアナログ入力で監視する方法」です。この資料では後者を扱います。おそらく後者のほうがメジャーだと思いますし、簡単なのでこちらを採用します。
ローパスフィルタ
ローパスフィルタは「低い周波数の信号を通し、高い周波数の信号をブロックする」働きをする電子回路の一種です。名前の通り、「ロー（Low）」＝低い、「パス（Pass）」＝通す、「フィルタ（Filter）」＝フィルタの役割をします。
音やデータ信号など、いろいろな種類の信号には「周波数」というものがあり、周波数は信号の「速さ」を表します。たとえば音楽の信号だと、低い周波数の音は「低音」に、高い周波数の音は「高音」に対応しています。
必要性
ローパスフィルタは、例えばノイズを減らしたいときに使います。ノイズは信号に混ざってしまう「不必要な高い周波数」のことが多いので、ローパスフィルタを使うことで高い周波数の成分を取り除き、必要な低い周波数だけを取り出すことができます。
また、音楽や音声の回路では、雑音や不要な周波数が音に悪影響を及ぼすのを防ぐためにも使われます。
ローパスフィルタの構成要素
ローパスフィルタは、主に「抵抗（Resistor）」と「コンデンサ（Capacitor）」で作られます。具体的には、抵抗とコンデンサを直列に接続し、コンデンサの片方の端をグラウンド（基準電位）に接続する簡単な回路です。このような回路は「RCローパスフィルタ」とも呼ばれます。
- 抵抗（R）
- 電流の流れを制限する役割を持ち、値が大きいほど電流を通しにくくします。
- コンデンサ（C）
- 電気を一時的に蓄えたり放出したりする役割があり、信号の変化をなだらかにします。
ローパスフィルタの動作原理
ローパスフィルタの動作を理解するためには、まず「周波数」と「リアクタンス（抵抗とは異なる特性で、周波数に応じて変化するコンデンサやコイルの性質）」を簡単に知っておくと役立ちます。イメージだけ以下にまとめました。
- 低周波数
- コンデンサは低周波数では信号を通すのを妨げません。そのため、低周波数の成分が回路を通過します。
- 高周波数
- 高周波数ではコンデンサがより強く信号を通しにくくなるため、信号が減衰（弱まること）されて通過しにくくなります。 結果として、低周波数の信号は通過し、高周波数の信号は抑えられることになります。
カットオフ周波数とは？
ローパスフィルタには「カットオフ周波数」という値があります。カットオフ周波数は、「どの周波数までを通過させ、どの周波数からをブロックするか」の境目を表す周波数です。この周波数は、抵抗値（R [Ω]）とコンデンサの容量（C [F]）で決まります。 \(f_c = \frac{1}{2 \pi RC} \mathrm{\, \left[Hz\right]}\) ここで、Rが大きいほどカットオフ周波数は低くなり、Cが大きいほど同様に低くなります。
ローパスフィルタの実際の使い方
- オーディオアンプ
- 音楽を再生するとき、不要な高周波ノイズを除去して、音質をクリアにするために使われます。
- センサー信号処理
- モータやセンサーから得られる信号がガタガタしたりノイズが入る場合、その高周波成分を除去して滑らかな信号にします。
- 電源回路の平滑化
- 電源に混入するノイズを除去し、安定した電圧を供給するために使われます。
自分で作ってみよう！
簡単なRCローパスフィルタを作ってみると、実際にどのように信号が変わるか体験できます。以下のような部品を用意しましょう：
- 抵抗器（たとえば10kΩ）
- コンデンサ（たとえば0.1μF）
回路を組み立て、入力側に信号（例えばPWM）を加え、出力側の信号がどのように変わるかをオシロスコープで確認すると、低い周波数が通過し、高い周波数が減衰する様子が観察できます。 ※ オシロスコープは高価なので岡田先生に使い方を聞きましょう
ボールセンサではどのように使うか
長々とローパスフィルタを解説してきましたが実際にどのように使うか解説していきます。ボールから送られてくる赤外線はセンサを通してパルス幅で出力されます。このパルス幅の変化を見るコートでボールの位置を割り出せます。しかし、Arduinoでこれを行うのは少しむずかしいです。そこで、ローパスフィルタを通してパルス幅の変化を電圧変化に変換します。使用する抵抗値は4.7kΩ、コンデンサの静電容量は10µFです。
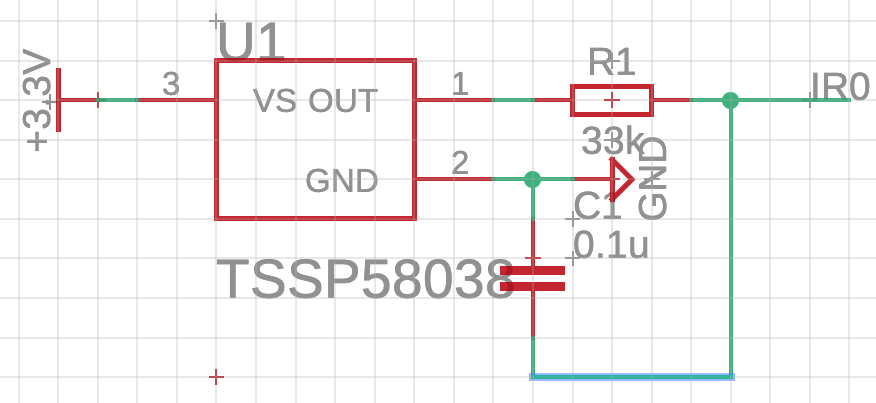回路CADでかいてみた回路が上の画像です。抵抗値とコンデンサの容量が異なっていますが多分どちらでも動くと思います。画像の中心あたりの長方形のシンボルが赤外線センサTSSP58038です。
- TSSP58038
- OUT
- 出力ピン
- ボールから受信したパルス幅が出力される
- VS
- 電源（3.3V）
- GND
- グラウンド 画像のIR0という部分をマイコンのアナログ入力で電圧を計測することでボールを探せます。出力電圧Vとボールとの距離lが一次関数で表せるので傾きと切片を実験で求めて上げれば大体の距離が算出できるようになります。
- OUT
ボールセンサを作る
赤外線センサとローパスフィルタを組み合わせて使う方法を解説してきました。ここからはそれを使ってボールセンサを作る方法を解説します。
角度を求める
赤外線センサの出力電圧がボールからの距離に比例するという前提のもとで考えていきます。
簡略化のためにセンサ数$n = 4$の場合で解説します。機体の中心を原点とした$xy$平面を考えます。赤外線センサ4個を半径$r$で等間隔に配置します。（それぞれが軸上に来るように配置するのが素直だと思います。）ボールの位置（$x_b$, $y_b$）、センサ$i$の出力電圧から算出したボールまでの距離を$l_i$とします。ボールが第一象限にある場合、センサ$1, 2$からボールまでの距離$l_1, l_2$が有効です。（本来センサ$3, 4$からはボールが見えないはずです。）
ボールまでのベクトルが$x$軸となす角$\theta$は$tan$の逆関数$arctan$を用いれば、 \(\theta = arctan(\frac{l_2+r}{l_1+r})\) となるはずです。センサの位置と向きの関係で、$l_1, l_2$を$x, y$軸の成分に分解する必要が無いので非常にシンプルな結果になります。また、機体中心からボールまでの距離$R$は、 \(R = \sqrt{(l_1 + r)^2 + (l_2 + r)^2}\) となります。（当然） $arctan$には慣れていないと思いますが、他の部分は非常に基礎的な内容なので理解しやすいのではないでしょうか？
$n=4$ では、円形ボールセンサの強みが殆どないので、一般化します。センサ$i$が座標$\left(r \cos\left(i * \frac{2 \pi}{n}\right), r \sin\left(i * \frac{2 \pi}{n}\right) \right) \quad (0 \leq i \leq n - 1)$ に配置されているとします。センサ$i$の出力電圧から求めたボールまでの距離を$l_i$とします。この時、センサ$i$からボールまでのベクトルを成分表示すると、$\left(l_i \cos\left(i * \frac{2 \pi}{n}\right), l_i \sin\left(i * \frac{2 \pi}{n}\right)\right)$となります。ここで、ボールの方向と逆方向にあるセンサたちの値は信用できません。そこで、ボールの方向にある$m$個のセンサの結果だけを利用することにします。ここでは、センサ$s_1, s_2, …, s_m$の値を利用するとしましょう。センサ$i$の位置ベクトルが$\left(r \cos\left(i * \frac{2 \pi}{n}\right), r \sin\left(i * \frac{2 \pi}{n}\right) \right)$であったことに注意して、ボールの$x成分, y成分$を足し合わせましょう。 \(x_{sum} = \sum_{i = 1}^{m}\left(r + l_{s_{i}}\right) \cos\left(s_i * \frac{2 \pi}{n}\right)\) \(y_{sum} = \sum_{i = 1}^{m}\left(r + l_{s_{i}}\right) \sin\left(s_i * \frac{2 \pi}{n}\right)\) 最後に、$theta$と$R$を求めてあげればボールのおおよその位置を求めることができます。 \(\theta = \arctan\left(\frac{y_{sum}}{x_{sum}}\right), \quad R = \sqrt{x_{sum}^2 + y_{sum}^2}\) $\theta$はかなり精度が出ますが、赤外線ボールの構造上、ボールの角度によって$\pm10$度ほどズレた気がします。$R$はかなりあてにならなかった気がします。詳しいことはここで解説されてます。
経験から、センサの個数は8~16個程度が良いと思います。それ以上センサを配置しても負担が増えるだけで精度はさほど向上しないです。また、アナログ入力でセンサの出力電圧を監視するので、マイコンのアナログ入力数が足りない問題があれば、ラインセンサの資料で解説しているアナログマルチプレクサ CD74HC4067を利用してみると良いと思います。
補正をする
先程も触れましたがボールの性質上、ボールの角度によって$theta,R$がかなりブレることがあります。これでは困るのでプログラムを工夫して、ブレを抑える必要があります。この資料では、移動平均について扱います。
移動平均フィルタの原理
移動平均フィルタは、一定数の過去データの平均をとることで、値の変動を滑らかにするフィルタです。例えば、最新の$n$点のデータを利用する場合、次のように計算します： \(\theta_{filtered} = \frac{1}{n}\sum_{i=0}^{n-1} \theta_i \quad※\) \(R_{filtered} = \frac{1}{n}\sum_{i=0}^{n-1} R_i\) ここで、$n$はフィルタのウィンドウ幅（データの数）です。ウィンドウ幅が大きいほど滑らかになりますが、応答が遅くなる可能性もあるため、適切なウィンドウ幅を選ぶ必要があります。
注意点
- 角度のラップアラウンド問題（※）
- θが360度（または2πラジアン）を超えるときに0に戻るため、直接移動平均を計算すると急激な変化が誤差として現れる可能性があります。
- 円周方向の平均などの手法があるようです
- 直線フィルタ vs 極座標フィル
- 場合によっては、極座標での移動平均よりも、x-y座標に変換してから移動平均を計算し、再度極座標に戻すほうが安定することがあります。
その他のフィルタ
- 指数移動平均（Exponential Moving Average, EMA）
- EMAは過去のデータよりも最新のデータに重みを置くことで、ブレを抑えながらも反応性の高いフィルタリングが可能です。移動平均よりも即時応答が得られるため、リアルタイム性が求められる場合に適しています。
- カルマンフィルタ
- 状態推定を行うカルマンフィルタは、ノイズの分散を考慮して、観測データと予測値を組み合わせて最適な推定を行います。Rとθに対しても適用可能で、過去の傾向やノイズモデルに基づいてより安定した値を得られます。
- メディアンフィルタ
- メディアンフィルタは、短期的な大きな変動やノイズを除去するのに有効です。例えば、過去の数点の中央値を取ることで一時的なノイズを抑えますが、移動平均よりも応答が鈍くなる場合があります。
それぞれのフィルタにはメリットとデメリットがあり、目的や求める精度によって使い分けることが推奨されます。まずは移動平均や指数移動平均で試してみるのが良いと思います。